全国第五届青少年信息学奥林匹克竞赛分区联赛初赛试题 [1999年]

1. 微机内的存储器的地址是以( )编址的。

2. 下列诸因素中,对微机工作影响最小的是 ( )

3. 在24*24 点阵的字库中，汉字“一 ”与“编”的字模占用字节数分别是（ ）

4. 将DOS 系统盘插入A驱动器启动机器，随后使用一批应用软件，在此过程中，DOS 系统盘 （ ）

5. 以下DOS命令中，有可能在磁盘上建立子目录的是 （ ）

6. 在CONFIG.SYS 文件中，装入特定可安装设备驱动程序的命令是 （）

7. 计算机能直接执行的指令包括两部分,它们是（）

8. 在微机中，通用寄存器的位数是 （）

9. 在计算机,字符编码通常采用( )

10. 计算机的软件系统通常分为 （ ）

11. 执行DOS 命令：C:\ATTRIB A: *.* 的功能是 （ ）

12. 执行下列DOS命令，效果等价的是 （）组

13. 已知小写字母“M”的十六进制的ASCⅡ码值是6D，则小写字母“C”的十六进制数的ASCⅡ码值是 （ ）

14. 计算机中的数有浮点与定点数两种，其中用浮点数表示的数，通常由（ ）这两部分组成。

15. 下列文件名中，属于DOS 中的保留设备名的为 （ ）

16. 启动计算机引导DOS是将操作系统 ( )

17. 十进制算术表达式 ：3*512 + 7*64 + 4*8 + 5的运算结果，用二进制表示为（ ）

18. 组成“教授”（JIAO SHOU）,“副教授”（FU JIAO SHOU）与“讲师”(JIANG SHI)这三个词的汉字，在GB2312-80字符集中都是一级汉字，对这三个词排序的结果是（ ）

19. 不同的计算机，其指令系统也不相同，这主要取决于 （ ）

20. 对具有隐含属性（H）的当前目录下的文件AB.TXT， 能成功执行的DOS命令是（ ）

1. 将Ln定义为求在一个平面中用n条直线所能确定的最大区域数目。例如：当n=1时，L1=2,进一步考虑，用n条折成角的直线（角度任意），放在平面上，能确定的最大区域数目Zn是多少？例如：当n=1时，Z1=2（如下图所示） 当给出n后，请写出以下的表达式： Ln = ______________ Zn = _______________
答案：n(n+1)/2+1|L2n-2n=2n2-n+1

1.

program exp1;  
var i,j,k:integer; a:array[0..100]of integer;
begin
  for i:=0 to 100 do a[i]:=i;
 for k:=5 downto 2 do
begin
      for i:=1 to 100 do if ( i mod k)=0 then a[i]:=0;
  for i:=1 to 99 do
     for j:=1 to 100-i do
 if a[j]>a[j+1]then  begin
          a[j]:=a[j]+a[j+1];
          a[j+1]:=a[j]-a[j+1];
          a[j]:=a[j]-a[j+1];
 end;
 end;
 j:=1;
 while (a[j]=0)and (j<100) do j:=j+1;
 for i:=j to 100 do a[0]:=a[0]+a[i];  writeln(a[0]);
 end.
输出：970

2.

设数组a[1]，a[2]，…，a[n]，已存入了数据，调用不同的排序程序，则数据比较的次数将会不同，试计算分别调用下列不同的排序过程的比较运算的次数。其中swap（i，j）表示a[i]与a[j]进行交换。
（1）proceduresort1（n：integer）；
var  i，j ：integer ；
begin 
      for  i：=1  to  n-1  do 
      for  j：=1  to  n  do 
if a[j] < a[i] then  swap (i,j) 
end; 
 调用该过程的语句为sort1（n），比较运算的次数为：__________

输出：n(n-1)

3.

proceduresort2（i，n：integer）；
var  j ：integer ；
begin
     if  i= n  then  write（a[n]）
else for  j：=i+1to  n  do
         begin
if  a[j] < a[i]  then  swap （i，j）
write（a[i]）；
sort2（i+1，n）
 end
end.
调用该过程的语句为sort2（1，n），比较运算的次数为：__________

输出：n(n-1)/2

4.

procedure sort3（i，j：integer）；
 var  m ：integer ；
begin
if  i〈〉jthen 
begin
  m：=（i+j） div  2 ；
  sort3（i，m）；sort3（m+1，j） ；
  merge ； { 假设合并的元素分别为p、ｇ个，需要比较p+ｇ次 }
  end；
 end；
调用该过程的语句为sort3（1，n），比较运算的次数为：__________

输出：nlog2n+c

1.
[问题描述]求一棵树的深度与宽度。共15分（2+2+3+2+2+2+2=15分）
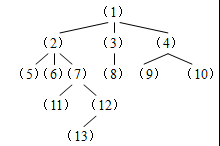
[算法说明]树可用数组tree:array[1..n,1..5]of integer;
其中：tree[I,1]表示结点号；tree[I,2]——tree[I,5]所属结点
如上图可表示为：
1 2 3 4 0
2 5 6 7 0
3 8 0 0 0
4 9 10 0 0
5 0 0 0 0
6 0 0 0 0
7 11 12 0 0
8 0 0 0 0
9 0 0 0 0
10 0 0 0 0
11 0 0 0 0
12 13 0 0 0
13 0 0 0 0
在求解的过程中，用到数组G:ARRAY[1..N,1..7]OF INTEGER；
其中：G[I,1]表示父结点，G[I,2]表示层次，
G[I,3]表示本结点号，G[I,4]——G[I,7]表示子女结点；
同时，设2个指针SP1（取数指针），SP2（存数指针）

program exGp3;
const n=13;
var i,j,k,sp1,sp2,n1,n2,jmax,p:integer;
 tree:array[1..n,1..5]of integer;
 g:array[1..n,1..7]of integer;
begin
 for i:=1 to n do 
  begin
 tree[i,1]:=i;
for j:=2 to 5 do read (tree[i,j]);readln;
  end;
 sp1:=1;sp2:=1;g[1,1]:=0;g[1,2]:=1;g[1,3]:=1;
 for i:=4 to 7 do g[1,i]:=tree[1,i-2];
 while sp1<=sp2 do
 begin
p:=g[sp1,2];n2:=g[sp1,3]; p:=p+1 ;j:=4;
while  g[sp1,j]<>0 do
begin
n1:=g[sp1,j];j:=j+1; sp2:=sp2+1 ;
g[sp2,1]:=n2;g[sp2,2]:=p;g[sp2,3]:=n1;
for i:=1 to 4 do g[sp2,i+3]:=tree[n1,i+1];
end;
  sp1:=sp1+1 ;
  end;
  writeln('maxd=',g[sp2,2]); j:=1;k:=g[1,2];jmax:=0;
  for i:=2 to sp2 do
  if k=g[i,2] then j:=j+1
 else begin
 if j>jmax then jmax:=j;
 j:=1  ;k:=g[Ｉ,2];
 end;
if j>jmax then jmax:=j;
writeln('max1=',jmax);
end.

2. [问题描述] 用生成法求出1，2，…，r的全排列(r<=8)（15分）（每个点3分）
[算法过程] 用数组：a:array[1..r]of integer ;表示排列；
初始化时，a[I]:=1(I=1,2,….f)
设中间的某一个排列为a[1],a[2],…a[r]
则求出下一个排列的算法为：
(1) 从后面向前找，直到找到一个顺序为止
（设下标为j-1,则a[j-1]<a[j]
(2) 从a[j]- a[r]中，找出一个a[k]比a[j-1]大的最小元素
(3) 将a[j-1]与a[Ｋ]交换
(4) 将a[j]，a[j+1]……a[r]由小到大排序。

  program exGp4;
 const r=7;
  var
  n,i,s,k,j,i1,t:intger;
  a  :array[1..r]of integer;
procedure print1;
  var 
 ik:integer;
  begin
 for ik:=1 to r do write(a[ik]:8);writeln;
  end
 begin
 for i:=1 to r do a[i]:=i  ;
 print1;
 s:=1;
 for i:=2 to r do s:=s*i;
 s:=s-1;
 for i:= 1 to s do 
begin 
j:=r;
while a[j-1]>a[j] do j:=j-1;
k:=j;
 for i1:=j+1 to r do 
 if (a[i1]>a[j-1]) and (a[i1]<a[k]) then k:=i1;
 t:=a[j-1];a[j-1]:=a[k];a[k]:=t;
 for i1:=j to r-1 do
for k:=i1+1 to r do
if  a[i1]>a[k]  then
 begin
t:=a[i1];a[i1]:=a[k];a[k]:=t;
 end;
 print1;
  　　　end;
  end.