全国第八届青少年信息学奥林匹克竞赛分区联赛初赛试题 [2002年]

1. 微型计算机的问世是由于( ) 的出现。

2. 下列说法中正确的是( ) 。

3. Windows98中,通过查找命令查找文件时,若输入F*.? , 则下列文件( ) 可以被查到。

4. CPU处理数据的基本单位是字,一个字的字长( ) 。

5. 资源管理器的目录前图标中增加"+"号,这个符号的意思是( ) 。

6. 下列哪一种程序设计语言是解释执行的( ) 。

7. 启动WORD的不正确方法是( ) 。

8. 多媒体计算机是指( ) 计算机。

9. 在树型目录结构中,不允许两个文件名相同主要是指( ) 。

10. 用画笔(Paintbrush)绘制图形并存储在文件中,该图形文件的文件名缺省的后缀为( ) 。

11. E-mail地址中用户名和邮件所在服务器名之间的分隔符号是( ) 。

12. (0.5)10=( ) 16.

13. IP v4地址是由( ) 位二进制数码表示的。

14. 算式(2047)10一(3FF)16+(2000)8的结果是( ) 。

15. 下列叙述中,错误的是( )

16. 一个向量第一个元素的存储地址是100,每个元素的长度是2,则第5个元素的地址是( )

17. 在所有排序方法中,关键字比较的次数与记录的初始排列次序无关的是( ) 。

18. 在计算机网络中,Modem的功能是( )

19. 设有一个含有13个元素的Hash表(O~12),Hash函数是:H(key)=key % 13,其中%是求余数运算。用线性探查法解决冲突,则对于序列(2、8、31、20、19、18、53、27),18应放在第几号格中( ) 。

20. 要使1…8号格子的访问顺序为:82、63、73、1、4,则下图中的空格中应填人( ) 。 1 2 3 4 5 6 7 8 4 6 1 -1 7 3 2

1. 如下图,有一个无穷大的的栈S,在栈的右边排列着1,2,3,4,5共五个车厢。其中每个车厢可以向左行走,也可以进入栈S让后面的车厢通过。现已知第一个到达出口的是3号车厢，请写出所有可能的到达出口的车厢排列总数(不必给出每种排列)。
答案：9

2. 将N个红球和M个黄球排成一行。例如:N=2,M=3可得到以下6种排法: 红红黄黄黄 红黄红黄黄 红黄黄红黄 黄红红黄黄 黄红黄红黄 黄黄黄红红 问题:当N=4,M=3时有多少种不同排法?(不用列出每种排法)
答案：35

1.

program exp1;
var i,j,k,n,,L0,L1,LK:Integer;
a :array [0..20] of integer;
begin
readln(n,k);
for i:=0 to n-1 do a[i]:=i+1;
a[n]:=a[n-1];L0:=n-1; Lk:=n-1;
for I:=1 to n-1 do
begin
 L1:=L0-k; if (l1<0) then L1:=L1+n;
If (l1=Lk) then begin
                 A[L0]:=a[n]; Lk:=Lk-1; a[n]:=a[Lk]; l0:=lk
                End;
Else
 Begin
     A[l0]:=a[l1];l0:=l1;
End;
End;
A[L0]:=a[n];
For I:=0 to n-1 do write(a[I]:4);
Writeln;
End.
输入:10   4
输出：7 8 9 10 1 2 3 4 5 6

2.

program exp2;
var n,jr,jw,jb:integer; 
ch1:char; 
ch:array[1..20]d char; 
begin
readln(n);
for i:=1 to n do read(ch[i]):
jr:=1;jwz=n;jb:=n;:
while (jr<=jw)do
begin
if(ch[jw]='R') 
then begin
ch1:=Ch[jr];Ch[jr]:=ch[jw];ch[jw]:=ch1:jr:=jr+13
end
else if ch[jw]='W'
then jw:=jw-1
else begin
ch1:=ch[jw];ch[jw]:=ch[jb];ch[jb]:=ch1;jw:=jw-1;jb:=jb-1;
end
end;
for i:=1 to n do write(ch[i]);
writeln;
end.
输入:10
RBRBWWRBBR
输出：RRRRWWBBBB

3.

Pmgram exp3;
Var I,j,p,n,q,s:integer;
a :array[1..20]of integer;
begin
readln(p,n,q);j :=21;
while (n>0)do 
begin
j:=j-1;a[j]:=n mod 10;n:=n div 10;
end;
s:=0;
for i:=j t0 20 do s:=s*p+a[i];
writeln(s);j :=21;
while (s>O)do
begin j:=j-1;a[j]:=s mod q;s:=s div q;end;
for i:=j to 20 do write(a[i]);readln;
end.
输入:7 3051 8
输出：1065
2051

1. 问题描述:将n个整数分成k组(k≤n,要求每组不能为空),显然这k个部分均可得到一个各自的和s1,s2,……sk,定义整数P为:
P=(S1-S2)^2+(S1-S3)^2+……+(S1-Sk)^2+(s2-s3)^2+……+(Sk-1-Sk)^2
问题求解:求出一种分法,使P为最小(若有多种方案仅记一种〉
程序说明:
数组:a[1],a[2],...A[N]存放原数
s[1],s[2],...,s[K]存放每个部分的和
b[1],b[2],...,b[N]穷举用临时空间
d[1],d[2],...,d[N]存放最佳方案
程序:

program exp4;
Var i,j,n,k : integer;
a :array [1..100] of integer;
b,d:array [0..100] of integer;
s :array[1..30] of integer;
begin 
readln(n,k);
for I:=1 to n do read(a[I]);
for I:=0 to n do b[I]:=1;
cmin:=1000000;
while (b[0]=1) do
begin
    for I:=1 to k do  s[i]:=0;    
for I:=1 to n do 
     s[b[i]]:=s[b[i]+a[i]];    
sum:=0;
for I:=1 to k-1 do
for j:=  i+1 to k do  
sum:=sum+(s[I]-s[j])*(s[I]-s[j]);
if    (cmin>sum)     then 
begin
cmin:=sum;
for I:=1 to n do d[I]:=b[I];
end;
j:=n;
while     (b[j]>k)      do j:=j-1;
b[j]:=b[j]+1;
for I:=j+1 to n do     b[i]:=1;     
end;
writeln(cmin);
for I:=1 to n do write(d[I]:4);
writeln;
end.

2. 问题描述:工厂在每天的生产中,需要一定数量的零件,同时也可以知道每天生产一个零件的生产单价。在N天的生产中,当天生产的零件可以满足当天的需要,若当天用不完,可以放到下一天去使用,但要收取每个零件的保管费,不同的天收取的费用也不相同。
问题求解:求得一个N天的生产计划(即N天中每天应生产零件个数),使总的费用最少。
输入:N(天数N<=29)
每天的需求量(N个整数)
每天生产零件的单价(N个整数)
每天保管零件的单价(N个整数)
输出:每天的生产零件个数(N个整数)
例如:当N=3时,其需要量与费用如下:

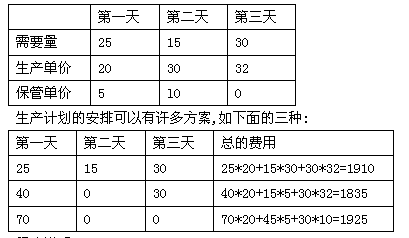
程序说明:
b[n]:存放每天的需求量
c[n]:每天生产零件的单价
d[n]:每天保管零件的单价
e[n]:生产计划
程序:

Program exp5;
Var
i,j,n,yu,j0,j1,s:integer;
b,c,d,e: array[0..30]of integer; begin
readln(n);
for i:=1 to n do readln(b[[i],c[I],d[i]];
fori:=1 to n do e[i]:=0;
   c[n+1]    :=10000;c[n+2]:=0;b[n+1]:=0;jO:=1;
while (jO<=n)do
begin
yu:=c[j0]; j1:=jO; s:=b[j0];
while    (yu+d[j1]<c[j1+1])    do
begin
     yu:yu+d[j1];     j1:=j1+1;s:=s+b[j1]; 
end;
  e[j0]:=s;       jO:=j1+1;
end;
for i:=1 to n do     write(e[i]:4);       
readln; 
end.