正规和枢轴
在一棵有根树中，每个顶点有一个正整数的权值。每个顶点要么是正规顶点(regular vetex)，要么是枢轴顶点(pivot vertex)。一个枢轴顶点的代价等于它的权值，而正规顶点的代价等于顶点权值减去它所有枢轴祖先中权值的最大值(当然代价不能小于0)。选择一个顶点成为枢轴顶点会增加当前的顶点处的代价，但同时可能会减少一些后代的代价。树的代价等于所有顶点的代价之和。

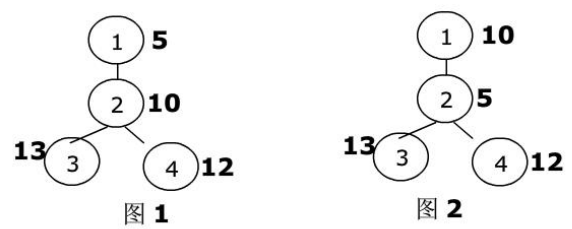
在图1中，选择2号点为枢轴顶点，3号和4号点为正规顶点(1号点任选)时，得到此树的最小代价为 5+10+(13-10)+(12-10)=20
在图2中，选择1号点为枢轴顶点，2号、3号和4号点为正规顶点时，得到此树的最小代价为10+0+(13-10)+(12-10)=15
以下程序假定所有结点依次编号为1~n，根为1号点，每个结点子女数不超过2个。
程序求得一棵有根树的最小代价，请将程序空白处补充完整。

program nbcz09_6; 
const maxn=5; 
var value:array[1..maxn]of longint;//value[j]表示第j点的权值 
    son:array[1..maxn,1..2]of longint;//son[j,k]表示第j点的第k个儿子的顶点号 
    n,i,x,y:longint; 
 
function min(a,b:longint):longint; 
begin if a<b then min:=a else min:=b;end; 
 
function max(a,b:longint):longint; 
begin if a>b then max:=a else max:=b;end; 
 
function caculate(a,b:longint):longint; 
var s1,s2:longint; 
begin 
   s1:=value[a]; 
   if son[a,1]<>0 then 
      s1:=s1+caculate(_____________); 
   if son[a,2]<>0 then 
      s1:=s1+caculate(_____________); 
   s2:=___________; 
   if son[a,1]<>0 then 
      s2:=s2+caculate(son[a,1],b); 
   if son[a,2]<>0 then 
      s2:=s2+caculate(son[a,2],b); 
   caculate:= _________; 
end; 
 
begin 
   readln(n);//n个点 
   for i:=1 to n do read(value[i]); 
   fillchar(son,sizeof(son),0);//son数组所有元素初值0表示开始没有儿子结点 
   for i:=1 to n-1 do begin//读入树的n-1条边 
      readln(x,y); 
      if ___________ then 
         son[x,1]:=y 
      else 
         son[x,2]:=y; 
   end; 
   writeln(caculate(_______)); 
end.